Если доступные вам ресурсы, например, время, деньги или пространство, ограничены, их нужно распределять наилучшим образом.
Предположим, что у вас есть помещение площадью 50 квадратных метров, которое можно использовать как склад. Ваш бюджет составляет 200000 рублей, и вы можете выбрать из множества шкафов всевозможных типов и размеров. Как оптимизировать имеющееся пространство, чтобы остаться в рамках выделенного бюджета?
Или допустим, что вы владелец нескольких грузовиков для доставки товаров и 10 пунктов погрузки-разгрузки. Как наиболее эффективно спланировать маршрут и расписание для этих грузовиков?
Или же представьте себе, что вы производите три продукта на основе одинакового сырья. Однако, поскольку в каждом продукте используется разное количество материала, производство некоторых из них обходится дороже, чем других. Некоторые материалы скоропортящиеся, и их необходимо использовать быстро. Сколько каждого продукта вы должны производить, чтобы минимизировать свои затраты? И в какой комбинации будет производиться минимум отходов?
Подобные вопросы могут показаться очень сложными: ведь нужно принять грамотное решение, учитывая множество переменных и ограничений. Ответ заключается в использовании линейного программирования.
Линейное программирование — это математический метод, который определяет оптимальный способ использования имеющихся ресурсов. Менеджеры используют этот процесс для принятия взвешенных решений о наиболее эффективном использовании ограниченных ресурсов, таких как деньги, время, материалы и оборудование.
Вы можете использовать линейное программирование только в том случае, если существует линейная зависимость между рассматриваемыми переменными. А это так, если единичное изменение одного фактора вызывает изменение другого фактора на постоянную величину. На графике линейная зависимость выглядит как прямая линия.
Метод линейного программирования
Чтобы упростить понимание линейного программирования, рассмотрим пример. Допустим, ваша компания производит два товара — куртки и пиджаки. Производительность ваших цехов составляет 525 часов в неделю. На пошив одной куртки уходит пять часов, а одного пиджака — три часа.
Потребительский спрос на пиджаки не ограничен. Покупатели готовы приобретать весь товар, который вы сможете произвести. С другой стороны, у курток максимальный спрос составляет всего 100 штук в неделю.
Ваши поставщики могут предоставить вам сырье, необходимое для производства не более 75 пиджаков в неделю. Сырье для курток находится в свободном доступе.
Прибыль на единицу продукции, или удельная валовая прибыль (В), составляет 2500 рублей для куртки и 2000 рублей для пиджака.
Сколько единиц курток и пиджаков вы должны производить еженедельно, чтобы получить максимальную прибыль?
1. Сформулируйте математическую задачу
Получить максимум:
В = 2500К + 2000П (максимальная прибыль).
С учетом приведенных выше ограничений:
5К + 3П ≤ 525 (ограничение производительности);
К ≤ 100 (ограничение продаж курток);
П ≤ 75 (ограничение количества сырья для пиджаков).
2. Отобразите проблему на графике
При наличии двух переменных (в нашем примере рассматриваются две комбинации товаров) можно составить график для поиска решения. Это отличный инструмент, помогающий полностью раскрыть вопрос. Если отложить производство курток по оси x и производство пиджаков по оси y, на вашем графике будут представлены максимальные производственные мощности для всех возможных комбинаций курток и пиджаков.
- Нарисуйте линию производительности.
Конечные точки линии производительности — это максимально возможное количество курток и пиджаков, которое может быть произведено.
Вы можете произвести:
105 курток (525/5) и 0 пиджаков (100,0)
или
0 курток (0,175) и 175 пиджаков (525/3).
Линия производительности соединяет эти две точки.
- Нарисуйте линию ограничения продаж для курток как К = 100 для всех значений П.
- Нарисуйте ограничение на сырье для пиджаков в виде П = 75 для всех значений К.
Эти три линии ограничений показаны ниже.
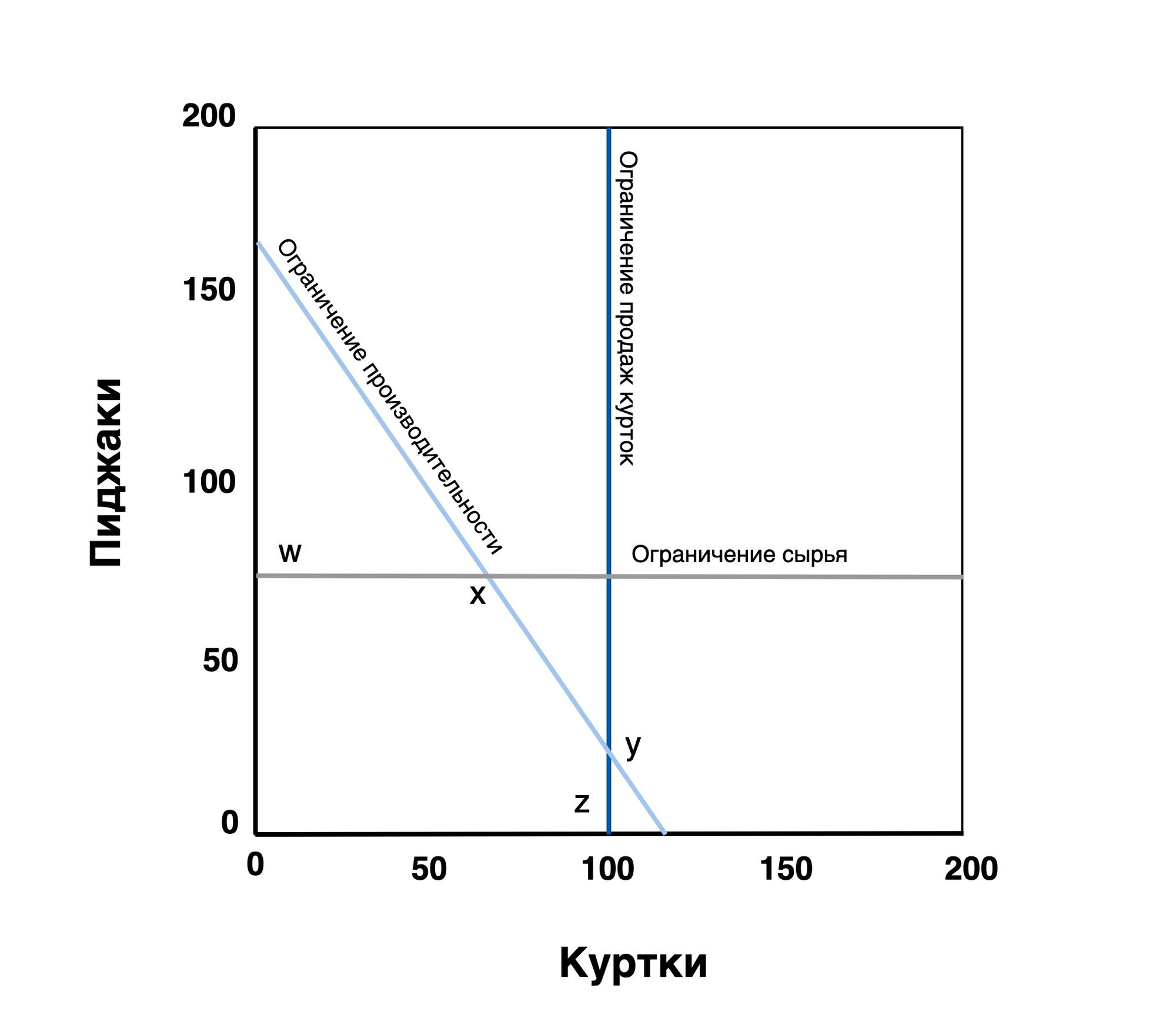
Граница, объединяющая три линии ограничений с осями x и y, представляет собой набор возможных комбинаций производства курток и пиджаков. Учитывая ограничения и предполагая ненулевой объем производства курток и пиджаков, все области вне этих границ не рассматриваются.
Оптимальная комбинация будет находиться где-то вдоль внешней границы. Область внутри границы не будет задействовать всю доступную производительность.
3. Рассчитайте оптимальное значение
Как узнать, в каком месте границы находится оптимальная точка? Она будет находиться на одном из пересечений различных линий ограничений. В этом примере есть четыре точки пересечения (w, x, y и z). Чтобы точно определить оптимальную точку, изучите каждую из них. Поскольку вы уже знаете, что w и z представляют собой крайние точки, используемые в линиях ограничений, можно рассмотреть приведенные ниже вычисления.
- Максимальная прибыль (В) в точке w
К = 0, П = 75;
В = 2500К + 2000П (максимальная прибыль);
В = (2500 × 0) + (2000 × 75);
В = 150000.
- Максимальная прибыль (В) в точке x
5К + 3П = 525;
П = 75.
Подставьте значение П в первое уравнение и решите его для К:
5К + (3 × 75) = 525;
5К = 300;
К = 60.
Итак, в точке x производство составляет 60 курток и 75 пиджаков:
В = 2500К + 2000П (максимальная прибыль);
В = (2500 × 60) + (2000 × 75);
В = 150000 +150000;
В = 300000.
- Максимальная прибыль (В) в точке y
5К + 3П = 525;
К = 100.
Подставим К = 100 в первое уравнение:
(5 × 100) + 3П = 525;
3П = 25;
П = 8 (округляем в меньшую сторону, потому что продать часть пиджака невозможно).
В = 2500К + 2000П (максимальная прибыль);
В = (2500 × 100) + (2000 × 8);
В = 250000 +16000;
В = 266000.
- Максимальная прибыль (В) в точке z
К = 100, П = 0;
В = 2500К + 2000П (максимальная прибыль);
В = (2500 × 100) + (2000 × 0);
В = 250000.
На основе этих расчетов определяем, что оптимальное производство курток и пиджаков находится в точке x (60 курток и 75 пиджаков).
Это простой пример линейного программирования. В реальной жизни большинство бизнес-задач связаны с таким количеством переменных и ограничений, что вы не возьметесь (или не сможете) решать их вручную. Для быстрого и удобного решения уравнений существуют программы линейного программирования; они предоставляют большое количество данных о различных точках в пределах возможного множества. Также можно запустить сценарии «что если», чтобы определить, например, какое дополнительное оборудование следует приобрести или следует ли привлечь еще одну смену рабочих.
